2023-01-28

第3回 RCO日本橋ハーフマラソン予選 B 問題 652K 解法解説

ainem さん (ainem (@ainemixion) / Twitter) 主催の第三回AHCをみんなで解く会コンテスト

github.com

に参加しました。この会は AHC のコンテストをチームを組んで解くというもので、今回は第3回 RCO 日本橋ハーフマラソン予選 B 問題が題材となりました。

問題 : B - ファーマーXの収穫計画
最終解答 : Submission #38248714 - 第3回 RCO日本橋ハーフマラソン予選

この会で 652K まで得点をのばし参加者中トップの得点を取れました。この記事ではこの解答について解説を行います。

考察

まずこの問題の状態として何をとればよいかというのを考えてみると以下となります。

手入れが終わってから収穫してよい
- 一度収穫すると 2 度と再収穫できないため、収穫 -> 手入れ -> 収穫という操作は無意味
手入れが終わった状態での最高得点は一意に決まる
- 手入れが終わった状態であれば盤面のどの連結区画が収穫可能かと各連結区画の収穫時の得点が固定される
- 各収穫に平等に 1 手必要なので得点の高い連結区画から収穫していけばよい

以上から各区画を何回手入れしたかというのを状態と定義してやれば、本問題のすべての解答をもれなくだぶりなく表現できそうです。

ここで問題の性質を考えるとこの問題には以下のような性質がありそうというのがわかります。

10 以上の品質は無意味
- 品質をあげるのは 1 操作 1 点にしかならない
  - そのうえ収穫困難になる
  - また 1 操作で 1 点をあげる方法はいくらでもある
    - 収穫対象にならない区画を適当に手入れして他の連結区画と連結させればよい
局所的な変更は大域的な影響をもららさない
- 最大の品質が 9 なので、ある区画の操作は 9 マス離れれば得点に影響しない
逆に局所的な変更はまわりの状況に非常に影響される
- ランダムに 1 区画選んで変更してもまず得点があがらない
- 組み合わせ最適化のうち、評価値があがる組み合わせが極端に疎となる問題というイメージ

方針

ランダムで盤面を変更する場合、複数の区画を同時に変更したほうがよさそうです。したがって以下のような山登りの方針なら (トップと戦えるかはともかく) 得点は伸ばせそうに見えました。

初期状態としてすべての区画の手入れ回数を 0 に
時間が尽きるまで (1950 msec の間) 以下を繰り返す
1. 区画をランダムに選択する
2. そこからランダムな数の区画をランダムに接続する
  - 接続する区画数は $[1\>選択された区画の品質初期値]$ からランダムに選ぶ
  - 接続する区画数はパラメータ調整対象。当初は $[3\>9]$ からランダムに選んでいた。
3. 接続した区画の品質が同じになるように手入れの回数を更新
4. 更新した手入れ回数の得点が元よりも高ければ保存、高くなければもとに戻す

これを実装したところ 500K 点ぐらいの得点でした。

差分評価

手元でタイムリミットをのばしてみると得点があがるので山登りしきれていなさそうです。上記の操作の処理時間を見てみると 0.4 msec 程度 (操作回数 5 千回) かかっていました。
いろいろな処理をコメントアウトして *1 みたところ、盤面の得点評価が圧倒的に時間がかかっていたので得点評価を高速化することを考えました。

考え方

考察の通り局所的な変更は大域的な影響をもたらさないので、局所的に変更した後に盤面全部を評価しなおすのは無駄となります。局所的な得点、つまり今の盤面で収穫可能な連結区画とその得点を管理すれば、変更した周辺だけを評価しなおして変更後の得点が計算できるはず、だと考えました。

手法

以下を管理して差分評価を実現しました。(map は実際には unordered_map を使っています)

各収穫可能な連結区画に番号をつける
- 区画がどの連結区画に所属するか (あるいは連結区画に所属しないか) は区画の座標を key として番号を value とする map (C++ でいうところの) で表現できる
- 逆のどの連結区画がどの区画を持つかは連結区画番号を key として連結区画に所属する区画リストを value とする map で表現できる
  - 連結区画を壊したときにどの区画に影響するかを見るのに必要
得点の管理として何点の連結区画があるかの multiset (C++ でいうところの) をもつ
- 総手入れ回数から収穫可能回数がわかるので、multiset の大きいほうから収穫可能回数個足しあわせれば得点が簡単に計算できる
- 注: ここは得点を key としてその得点を達成する連結区画数を value とする map をもってもよかったかもしれないです
連結区画の得点を管理するために連結区画番号を key として得点の map をもつ
- 連結区画を壊したときに何点下がるかを簡単に計算するため
- 注: これは不要でした (得点は連結区画の区画リストの区画数から容易に計算可能)

更新手順

更新するときは影響の受ける連結区画を慎重に見定める必要がありました *2。以下の手順で操作を行えば更新による収穫できる連結区画の増減を漏れなく検知できます。

更新対象の区画が所属する連結区画を列挙する
列挙した連結区画を破棄する
- 連結区画の得点も破棄しておく
更新対象の区画 + 破棄した連結区画に所属する更新対象外の区画に対して収穫できる連結区画ができるかチェックする
チェックの結果収穫できると判明した連結区画に新たな番号を振る
- 新たな連結区画の得点を記録する

高速化効果

差分評価を実装したところ、操作にかかる時間は 8 microsec ほど (操作回数 25 万回) となりました。およそこれで 600K 点ほどです。

山登り解の改善

この解答は乱択なため、できあがりの盤面は無駄が含まれていていくらかの改善ができます*3。

収穫できない区画への手入れを解除
- 無駄な手入れ回数を収穫にまわす
ある区画が連結区画に属していて、品質の低い別の連結区画に隣接している場合、手入れ回数を減らすして所属する連結区画を変更する
- 手入れ回数が 0 未満にならない場合に限る
- 減らした手入れ回数分を収穫にまわせる
ある区画が連結区画に属していないが何回か手入れを行えば連結区画に連結できる場合、得点の状況を考慮しながら手入れを行う
- 手入れを行うと別の連結区画が収穫できなくなるため $\frac{増加得点}{手入れ回数}$ と収穫対象の連結区画の最低得点を比較しながら手入れを行うかどうかを決める
最後に連結区画に対して $得点効率 = \frac{得点}{総手入れ回数 + 1}$ 順にならべて得点効率の悪い連結区画の手入れを解除する

以上の貪欲改善を行うと 1 テストケースにつき 100 点弱プラスでき、総計で 650K 点となりました。

得点状況

seed=1 に対する得点状況は以下のようになりました。2 点の区画まで収穫しているようです。

初期状態

操作後

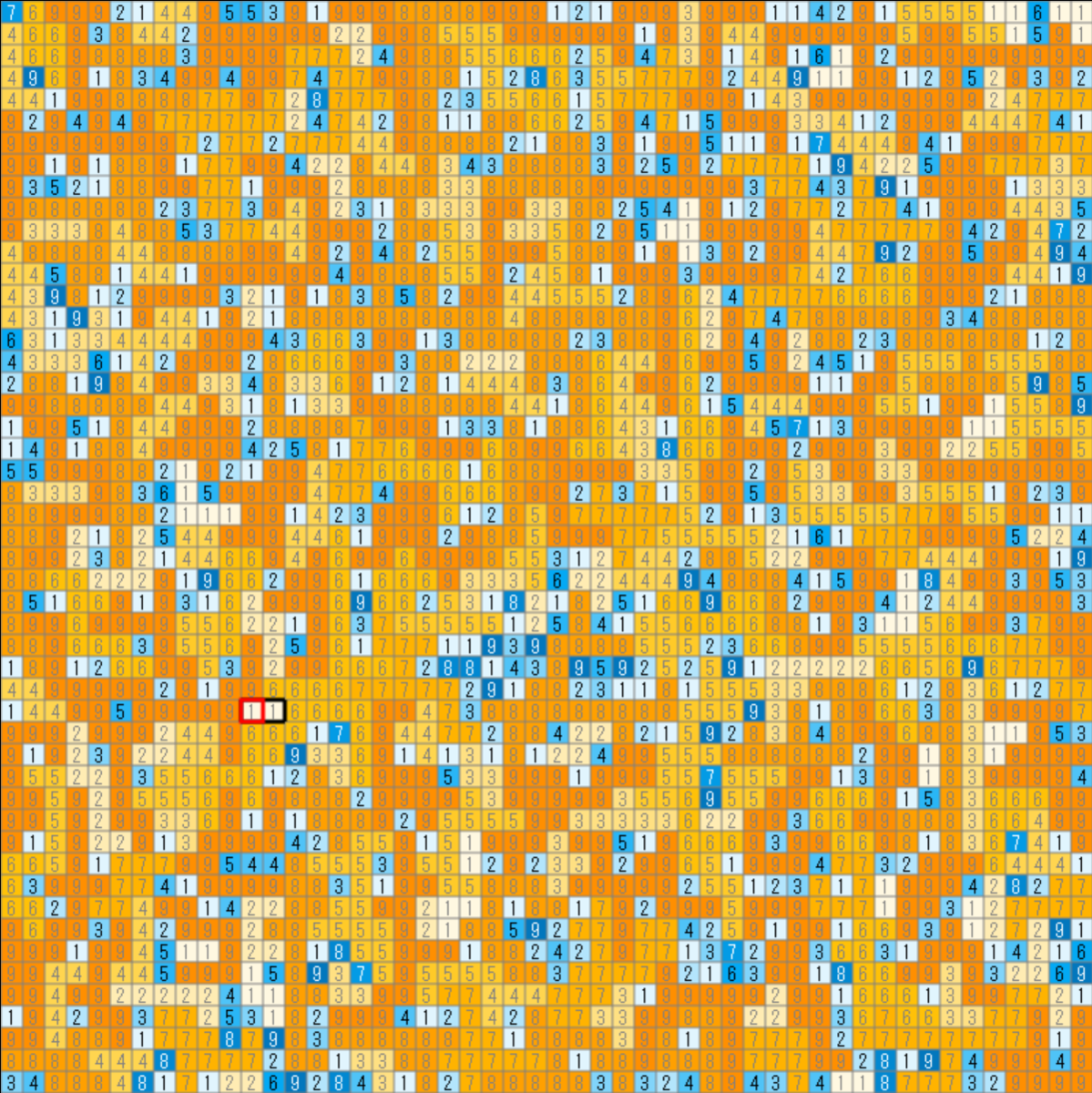
好スコア要因

連結区画が十分作れてすべての連結区画を収穫できなくなった状態において、得点が上がる方向への遷移を考えると以下のようになっており、自然と得点効率があがる方向に遷移していったので好スコアが出たのだと考えています。

無駄に手入れするのをやめる
- 例えば初期品質 1 の区画を手入れして他の連結区画に連結していたのを手入れ回数を 0 にする
  - もとの連結区画が収穫できる状態を保つこと
- 手入れ回数が減る分収穫回数があがって得点アップ
大きな初期品質の区画を他の連結区画に連結する
- 得点増加分と手入れ回数増加による収穫回数減少分を考慮しても得点アップする場合のみ

焼きなましが上手くいかなかった原因

山登り関数の名前が annealing になっている通り当初は焼きなましをしようとしていました。ただしやってみたところ得点がのびずまったく焼けませんでした。本解答の更新手法は近傍状態への遷移と考えてよいですが、近傍状態のうち得点が増えるものが極めてすくないため、焼きなましを行うとどんどん得点が失われていくようです。

おわりに

ainem さん、楽しい会を開催していただいてありがとうございます。

*1:面倒だったのでコメントアウトでボトルネックをみました。よい子はちゃんとプロファイラなり計測コードなりで測りましょう。

*2:バグの退治に苦労しました

*3:このあたりは最後にやったので詰め切れていないです

2020-09-20

REP マクロの罠

プログラミング競技プログラミング

本日の ABC 179 E　の愚直解

#include <iostream>
#include <vector>
#include <cinttypes>

#define REP(n) for (int repeat_index = 0; repeat_index < (int)n; repeat_index++)

using namespace std;

int main()
{
    int64_t n, x, m;
    cin >> n >> x >> m;

    int64_t sum = 0;
    REP(n) {
        sum += x;
        x = x * x % m;
    }
    cout << sum << endl;

    return 0;
}

は TLE ではなく WA となります。実行結果

愚直に計算しているだけなのになぜ合わない？となったのですが、実は REP マクロの中の n との比較に int へのキャストが入っているため、1.0E10 が上限の n に対してはリピート回数は n とは限らないのでした...。int へのキャスト自体は別の問題で型不整合により間違いを引き起こしたために入れておいたのですがこれが裏目に出たようです。

REP マクロは以下のように decltype で型をあわせるのがよさそうです。

#define REP(n) for (decltype(n) repeat_index = 0; repeat_index < (int)n; repeat_index++)

2020-09-13

AtCoder ABC178 参戦記

AtCoder の ABC178

atcoder.jp

に参加しました。

結果は 62 分全完 (1 WA) 134 分でパフォーマンス2275でした。ここ三回連続黄パフォを出せているので、この調子でがんばっていきたいと思います。

f:id:y_r:20200913233050p:plain

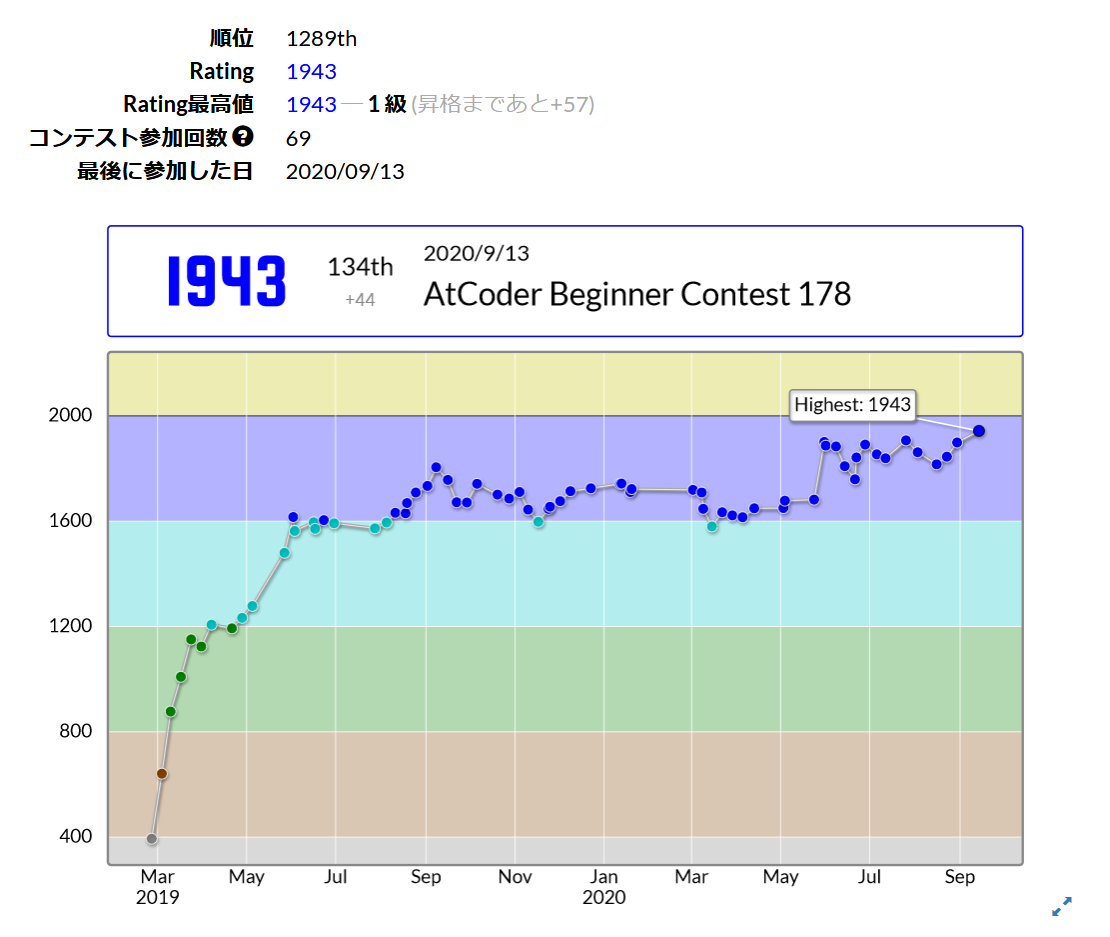
感想

A 問題

(1 - x) でよい。業務でも時々書く。

B 問題

(a * c) or (b * c) or (a * d) or (b * d) のどれかが最大値を与えるので全部実行して max を取る。

C 問題

DP に訴える。各桁を見て行ったときに以下のように状態を割り振れば遷移は簡単に書ける。

dp[i][0] : (0, 9) もない
dp[i][1] : 0 がある
dp[i][2] : 9 がある
dp[i][3] : 0 も 9 もある

D 問題

これまた DP。dp[i] を s = i のときの個数とすると以下のようになる

$dp[i] = \sum _{j=1}^{i - 3} dp[j] + 1 (i >= 3)$

E 問題

y で降順ソート
左候補と右候補をトラッキングしながら各点を処理
- 点と左候補、点と右候補の距離を計算
- 左候補に対して diff(-x) >= diff(-y) なら左候補を置き換え
- 右候補に対して diff(x) >= diff(-y) なら右候補を置き換え

典型っぽいので "点群マンハッタン距離" で検索したくなった。

F 問題

A と B に同じ数値が n 個よりおおくある場合は NG (無証明)。構築は以下のようにして行う

数値が入っていないポジションを set で管理
A にある数値のうち (A での個数 + B での個数) が多い順から処理
- - A でのポジションの直後から数値を入れられるポジションに B の個数分数値を入れる
B にしかない数値をあてはめていく

2020-09-12

ACL を VisualStudio で読み込んだときにビルドエラーが出たので対応した

AtCoder のライブラリ ACL

atcoder.jp

を VisualStudio で読み込もうとしてビルドエラーにであったので対応法を書いておきます。

症状

#include <atcoder/all>

とすると以下のエラーになります。

1>C:\work\atcoder\atcoder\atcoder\acl\atcoder\internal_math.hpp(49,9): error C3861: '_umul128': 識別子が見つかりませんでした

対応法

ビルドプラットフォームを x86 にしているのが原因なので x64 に変更すればよい。

参考 : _umul128 | Microsoft Docs

組み込み  アーキテクチャ Header
_umul128 x64                 <intrin.h>

2020-01-19

AtCoder キーエンスプログラミングコンテスト 2020 参戦記

プログラミング競技プログラミング

AtCoder キーエンスプログラミングコンテスト 2020

atcoder.jp

に参加しました。

結果は 33 分 ABC 2 WA で 993 位パフォーマンス　1384 でした。ここ数回ちょっとずつ上げたレートを吐き出す結果になりました。夕食が家族そろっていて飲んでいたので仕方ない*1ですね...

f:id:y_r:20200119115643p:plain

感想

A 問題

縦か横か升目の多い方を選んで規定数を超えるまで塗りつぶす。

B 問題

200 点!!? 400 点ぐらいに見えた。
左腕をソートして順番に見ていく。

現在有効なロボットがない場合は今のロボットを有効なロボットに設定
現在有効なロボットがある場合は、今のロボットの右腕が現在有効なロボットより小さければ今のロボットを現在有効なロボットとする
現在有効なロボットは右腕の期限で失効

区間スケジューリング問題という有名問題らしい。

なお、最初制約を一桁小さく見て $O(N^2)$ 解を投げて TLE くらった。

C 問題

気づくとギャグ問題。K <= N なので先頭から K 個 S をつなげればよい。あとは S+1 でも並べとけばよいが、S が 10^9 のときだけ 1 を並べる。
最初 S + 1 が 10^9 となるときに 1 を並べて WA をくらった。

D 問題

最初任意のカードを交換できると誤読していてだいぶ時間を溶かした...

各カードの表裏は $2^{18}$ なので全通り試せる
各カードの表裏が決まるとそのカードの数値が決まり、おける場所は奇数番目か偶数番目に拘束される
表裏を固定して実現可能か見て実現可能なものの操作回数の最小値が答え
- 実現可能かは、裏表決め打ちしたカードをソートして適切な位置にあるか見る
  - 同じ数値のカードがある場合は、奇数番目偶数番目を守ったうえで、ソート前に先頭にあるカードから並べていく
操作回数はバブルソートと同じ (=転倒数) でナイーブに計算しても $O(N^2)$ $N <= 18$ で瞬殺

...考察はあっていたが同じ数値のカードをいじるところで無限にバグを出し続けてタイムアップだった。twitter で見るようにおける場所の奇数偶数にわけてソートした方が楽だった。

E 問題

寝ている間に (誤読しつつも) 考察が降ってきたので起きてから通した。D より簡単だったかも...

$D$ で昇順ソート
の小さい方から
- 隣接頂点に色を塗っている頂点がなければ、[tex :D] の最小値を持っている隣接頂点を選び出す
  - このとき 2 頂点の最小値が等しくなければ構築不可能
  - そうでなければ 2 頂点を白黒に塗り分けて間の辺のコストに今の頂点の $D$ をいれる
- 色を塗っている頂点があればその頂点とは違う色を今の頂点に塗って、その間の辺のコストを今の頂点の $D$ に設定する
残りの辺のコストは無限大 (実際には最大値) をいれておく
上記でよいのは昇順ソートしてあるので、色を塗り済みの頂点に新しい辺のコストを設定してもその頂点の最小値には影響しないため

誤読は最小値が各頂点に拘束されているのを読み落としていたこと。提出して RE, WA 祭りになって気が付いた。

*1:B, C での WA はともかく D のバグが取れなかったのは言い訳が聞かない

2020-01-13

AtCoder ABC 151 参戦記

プログラミング競技プログラミング

AtCoder ABC151

atcoder.jp

に参加しました。

結果は 92 分全完でしたが 6 WA くらい、しかも全完の人数が多かったため 443 位パフォーマンス 1745 でした。
いろいろ無駄に溶かしたのがもったいなかったですね。

f:id:y_r:20200112235437p:plain

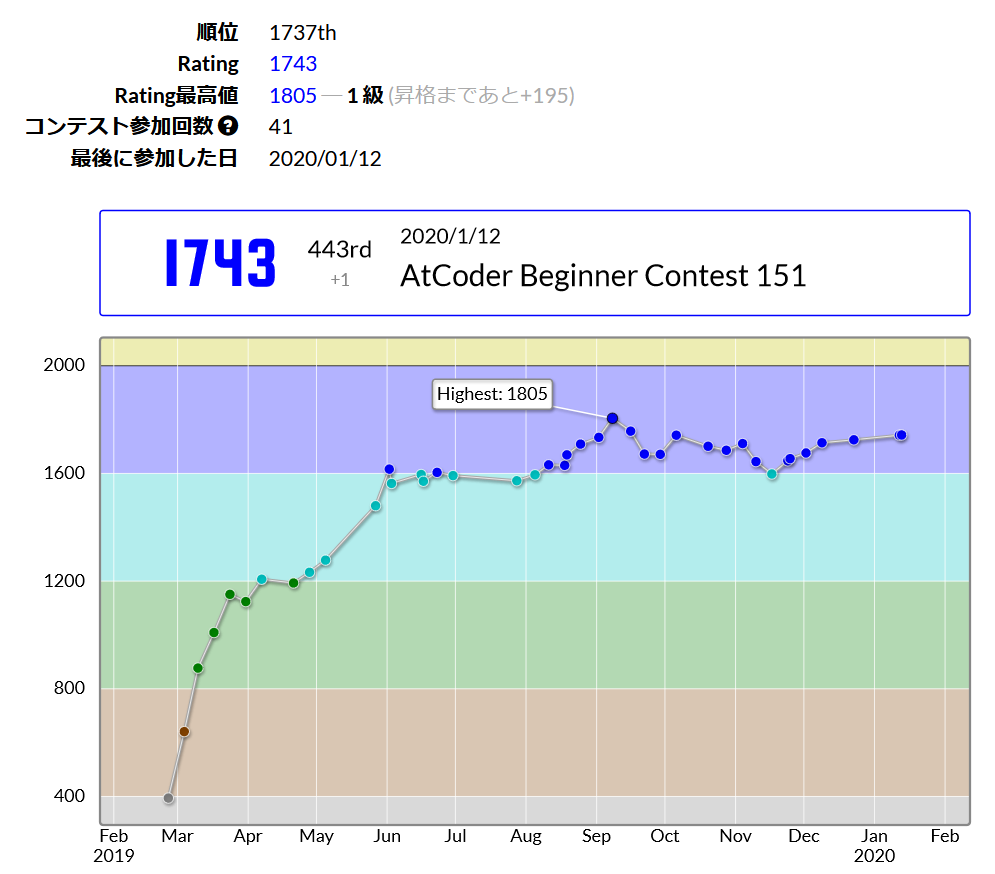
感想

A 問題, B 問題

やるだけ

C 問題

AC の数と AC までの WA を数えればよい...が AC していない問題の WA も数えてしまい +1WA

D 問題

六重ループが間に合うので (開始点、終了点) を全探索する。
探索コードはいつもいちいち書いているがライブラリ化したほうがよいのだろうか？

E 問題

ソートしてほしそうに見えるのでソートする
最小値については $i$ 番目
最大値についても同様

だが、mod の計算を間違えて +1WA してしまった。

引くときは法を超えるのは考えなくてよいと思ったのだが...

F 問題

3 点を通る円 or 2 点を通る最小円が候補
上記は全探索できる
2 点を通る最小円は自明
3 点を通る最小円は適当にぐぐればよい
- "外接円" のキーワードを思い出せなかったためにだいぶ損をした*1

最初 2 点を通る円が候補になるのに気が付かずに 3 点での結果の誤差判定をいじって投げつけていたため 4 WA くらってしまった...

※ 最小包含円 | libalgo という有名問題だった模様

*1:まあ高校受験したのが 20 年以上前なので仕方ないですね

2020-01-12

第6回ドワンゴからの挑戦状予選参戦記

プログラミング競技プログラミング

AtCoder の第6回ドワンゴからの挑戦状予選

atcoder.jp

に参加しました。

結果は 70 分でAB が解けて 360 位パフォーマンス 1883 でした。600 取れたからいいようなものの 200 - 600 - 800 - 800 は辛かった...

f:id:y_r:20200112144853p:plain

感想

A 問題

文字列とマッチさせてそれ以降の数値を足すだけ。

B 問題

$期待値 * 発生数$ が回答なので、全通りの移動量を回答すればよい。
位置の差分を $d_i (0 <= i < N)$ とし、 $d_i$ を通る全スライム数を $C_i$ とすると回答は $\Sigma(d_i * C_i)$
の数え方だが
- ひとつ左のスライムが通る回数は全通りなので $(N-1)!$
- ふたつ左が通る回数 + ... を足し込めばいいがよくわからん
- しかたないので実験してみると個左のスライムが通る回数は
  - $N=4$ : $6, 3, 2$
  - $N=5$ : $24, 12, 8, 6$
  - $N=6$ : $120, 60, 40, 30, 24$
- 上記をにらんでると位置 $k$ に対して $\sum^{k}_{l=1}(((N-1)!)/l)$ が見える

で AC。あとから考えてみると以下がなりたっている。

とあるスライムが 2 個以上右に移動するのは右隣のスライムの後に選ばれた場合でこれは確率
- 他のスライムとは関係なく問題のスライム間の順序なので、2 個のスライムのうち特定のスライムが後に選ばれる確率となる
同様に $k$ 個以上右に移動するのは右隣 $k-1$ 個のスライムのなかで一番後に選ばれた場合で確率 $1/k$

C 問題

見たけどわかりません。

D 問題

なんか貪欲が見えるけど、構築する手順が見えなかった。
なお、終了直後に投げた深さ探索回答は無事 TLE だった模様...